Ranking metrics: pitfalls and best practices

Positional discount in ranking metrics creates subtle complexities. Parameters like K values and relevance levels significantly impact model training and evaluation, requiring careful consideration. This post explores how metrics like MRR and NDCG handle position-based discounting and examines common pitfalls in their practical implementation.
ML
Learning-to-rank
Author

Hongsup Shin

Published

February 8, 2025

Code 
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format='retina'
plt.style.use('ggplot')

Ranking is everywhere. When you search for products online or scroll through your social media feed, you’re interacting with ranking systems. Unlike classification where we simply predict a category, ranking requires ordering items by their relevance or importance. This fundamental difference requires specific metrics so-called information retrieval (IR) metrics that capture nuanced aspects of ranking quality. Choosing the right ranking metric requires good understanding of reward, discount, and normalization of ranking metrics. In this post, we will discuss mathematical properties of various ranking metrics, focusing on common pitfalls in practice and how to address them. Let’s start with some basics.

Why ranking is different

A good way to understand ranking is to compare it against classification. Let’s say we have a dataset with three relevance grades: excellent, good, and mediocre. We can train a multi-class classifier to predict the probability of a sample belonging to each grade. In learning-to-rank (LTR) framework, this is called point-wise ranking approach. However, at the core, ranking is about understanding relative relationship among different samples, and thus, more preferred LTR models take pair-wise or list-wise approach.

This consideration of multi-sample comparison is related to how LTR is used in practice. When retrieving relevant documents or optimizing search query, we work with multiple queries. This means, we want to generalize the model to learn the relative importance of samples across multiple datasets. This is why a typical LTR dataset contains a group variable that indicates group or query membership. This also means that in some groups, we might not always have all relevance labels. For instance, in the three-grade example, we might have a query group where we only have samples that belong to “excellent” and “mediocre”, without the “good” grade. A classifier will complain about this but LTR optimization loss can naturally handle this.

Finally and most importantly, ranking deals with positional bias. We can train a model that optimizes the ranking of all items in a dataset, but in practice, we normally care about the small minority at the top (i.e., top K). This leads to more complex use cases and metrics such as whether only the top first item matters or top 10 items, or how we penalize model when it makes errors. Related to this, compared to classification, partial correctness exists in ranking systems. Even when model prediction does not result in a perfect ranking, loss can be computed by considering how far it is from the ideal ranking.

Mean reciprocal rank (MRR)

Ranking metrics are naturally designed to digest the positional information (ranks) of relevant items retrieved. Mean reciprocal rank (MRR) is a good example where the metric is solely computed by ranks. Mathematically, MRR is defined as:

\[ \text{MRR} = \frac{1}{|Q|} \sum_{i=1}^{|Q|} \frac{1}{\text{rank}_i} \]

where \(\text{rank}_i\) refers to the rank of the first relevant item of \(i\)th query from a set of queries, \(Q\). In other words, MRR is the inverse of the harmonic mean of ranks of the first relevant items. This also indicates that MRR’s focus is a single item, not the overall quality of ranking of an array.

Hyperbolic discount of reward

Since we use reciprocal rank (RR), \(\frac{1}{\text{rank}_i}\), individual RR scores shows hyperbolic decay:

Code 
fig, ax = plt.subplots(1, 1, figsize=(4, 2.5))
ax.plot(1 / np.arange(1, 100))
ax.set(xlabel="Rank of the first relevant item", ylabel="RR score")
fig.tight_layout()
Figure 1: Hyperbolic decay of reciprocal rank (RR)

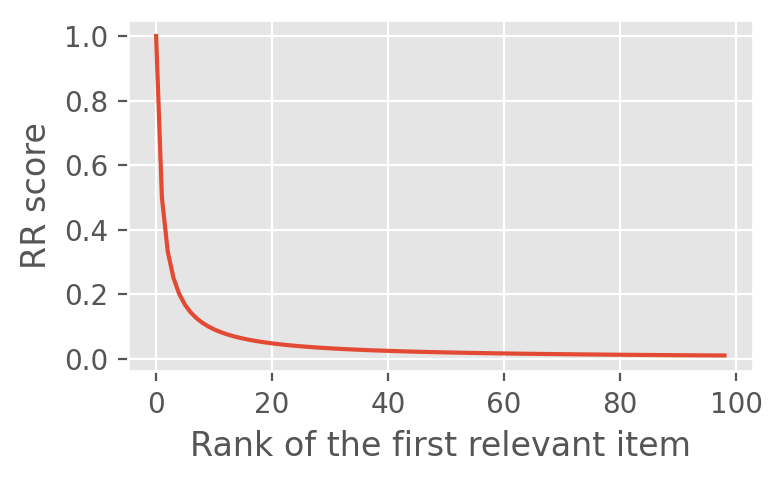
This hyperbolic decay means the RR score difference between \(i\)th and \(i+k\)th item is much larger when \(i\) is small. For instance, the difference between getting the relevant item in the first vs. second place is much larger than getting the relevant item in the 100th vs. the 101st places.

This positional reward discount in RR is a core characteristic of most ranking metrics. In ranking systems, we put more emphasis on low ranking values. When ranking quality is poor (higher ranking values), discerning the ranking performance in this region is less meaningful than in the lower-ranking region.

Harmonic nature of MRR

This positional discount is why we use harmonic mean of ranks in MRR. When we compute the average of RR scores across queries, we do not want to equally treat a query with RR score of 1 (i.e., getting the relevant item in the 1st place) and a query with RR score of 0.2 (i.e., 1/5, getting the item in the 5th place).

On one hand, this means MRR is less sensitive to outliers: MRR does not change dramatically with occasional bad ranking performance because its contribution is small. But on the other, this implies that a small number queries with low rank values (high RR scores) can significantly outweigh multiple queries with higher rank values.

Assume that we have 4 queries, and system A returns the first relevant item at ranks 2, 3, 2 and 3, respectively, while system B returns the relevant items at ranks 1, 10, 1 and 15:

def MRR(ranks):
    return round((1 / ranks).mean(), 4)


first_relevant_ranks_A = np.array([2, 3, 2, 3])
first_relevant_ranks_B = np.array([1, 10, 1, 15])

print(f"MRR(A):{MRR(first_relevant_ranks_A)}")
print(f"MRR(B):{MRR(first_relevant_ranks_B)}")
MRR(A):0.4167
MRR(B):0.5417

In this example, MRR score is higher in system B but the overall ranking quality is more consistent in system A, which is likely to be preferable in practice. This suggests MRR alone is not enough, and it is useful to understand the distribution of individual RR scores.

Normalized discounted cumulative gain (NDCG)

NDCG is perhaps the most widely used ranking metric. Compared to MRR, NDCG has two distinctive features:

  • It evaluates overall quality of ranking, not just the location of the first relevant item.
  • It can incorporate graded relevance levels where item relevance grades are more granular than binary.

NDCG is a normalized form of DCG. DCG is defined as:

\[DCG_K = \sum_{i=1}^K \frac{2^{rel_i} - 1}{\log_2(i + 1)}\]

where \(rel_i\) represents the relevance of the \(i\)th item and \(K\) is the size of top-ranked items we consider (i.e., K in top K). NDCG is a normalized form of DCG: we divide DCG by ideal DCG (IDCG), which can be only computed when we have full knowledge of the ranking labels so we know what the ideal order of all items is:

\[NDCG_K = \frac{DCG_K}{IDCG_K}\]

Linear vs. exponential gain

There are actually two versions of DCG implementation. The one above is more commonly used in industry and research, and it uses exponential gain on the numerator. The original DCG formula on the other hand, uses linear gain:

\[DCG_K = \sum_{i=1}^K \frac{rel_i}{\log_2(i + 1)}\]

As of now (Feb 2025), the scikit-learn (ver. 1.6) uses the linear gain in NDCG calculation. So if we want to compute NDCG scores using sklearn, it’s important to know that its linear calculation of the score is going to be often different from the exponential version, which modern ML model packages use. For instance, in LightGBM, the loss objective xe_ndcg (or rank_xendcg) based on Bruch 2021 uses the exponential gain.

import sklearn
from sklearn.metrics import ndcg_score

print(f"sklearn version:{sklearn.__version__}")


def dcg(relevance_labels, scores, gain_type):
    ranking = np.argsort(scores)[::-1]
    relevance_labels_ranked = relevance_labels[ranking]
    if gain_type == "linear":
        gains = relevance_labels_ranked
    elif gain_type == "exponential":
        gains = 2**relevance_labels_ranked - 1
    discounts = np.log2(np.arange(1, len(scores) + 1) + 1)
    return np.sum(gains / discounts)


y_true = np.array([10, 0, 0, 1, 5])
scores = np.array([0.1, 0.2, 0.3, 4, 70])
ndcg_sklearn = ndcg_score(y_true.reshape((1, -1)), scores.reshape((1, -1)))
ndcg_lin = dcg(y_true, scores, "linear") / dcg(y_true, y_true, "linear")
ndcg_exp = dcg(y_true, scores, "exponential") / dcg(y_true, y_true, "exponential")

print(f"NDCG with scikit-learn    : {ndcg_sklearn:.4f}")
print(f"NDCG with linear gain     : {ndcg_lin:.4f}")
print(f"NDCG with exponential gain: {ndcg_exp:.4f}")
sklearn version:1.6.0
NDCG with scikit-learn    : 0.6957
NDCG with linear gain     : 0.6957
NDCG with exponential gain: 0.4097

In the exponential version, higher relevance scores are emphasized much more strongly than the linear one. This is certainly better for applications where finding highly relevant items is critically important. This explains the difference in NDCG scores between linear and exponential in the above example. In our example, the relevance scores [10, 0, 0, 1, 5] range from 0 to 10 and exponential gains of 10 and 5 are massive. Therefore, any suboptimal ordering, which the example provides, is heavily penalized.

NDCG comparison: The importance of fixed K

One common mistake when comparing NDCG scores of top K items (NDCG@K) is to compare the scores across different Ks. For instance, one might want to compare NDCG@5 vs. NDCG@10. This should be avoided.

NDCG with different Ks are two fundamentally different cases. For a smaller K, the score calculation ignores candidates with ranks larger than K, which will be considered when computing NDCG with a larger K. Also, the discounting effect from \(\log_2(i+1)\) in the denominator causes errors at different positions have different impacts. Since later positions have less impact on the final score, NDCG score at a larger K can sometimes be higher even with mistakes in the tail region. Finally, since NDCG is a normalized metric, when K differs, the normalization term also changes. This means NDCG comparison with different K ignors the scaling difference.

Thus, when we evaluate different ranking systems and models, we should always compare NDCG scores at the same K value. However, since NDCG with a fixed K provides a single snapshot of the ranking quality at a given K, it is recommended to report NDCG at multiple K values to understand the model behavior in depth. Using other metrics such as MRR or mean average precision together is even better.

Why small K

When choosing K, the main consideration should be the use case of the system. For search query or video recommendation, K should be small because users only care about top 1-5 items. But for a use case like song playlist generation, K can be a bit larger than that. This means we need to consider how users interact with the system.

There are computational and modeling aspects that discourage having a larger K as well. First, as MRR and NDCG show, ranking metrics come with positional discount. Later positions have minimal impact and ranking error in this region may not provide much signal for models to learn. It’s even possible that models might focus on minor improvements in deep positions instead of focusing on top positions, which eventually can lead to slower convergence. In addition, as we saw in the examples above, as K becomes larger, there are more subtle nuances that occur, which evaluation metrics or losses might not be able to fully capture. This makes evaluation at larger K values less reliable. And of course, a larger K requires more compute resources.

So it is often more sensible to keep the size of K small. If we have a use case where K is large, we need to think about whether ranking is the best approach here. Alternatively, we can propose a solution where K can be kept small. For instance, instead of suggesting top 100 videos to a user group at once, we can recommend top 5 videos per user.

Granularity in relevance levels

When defining relevance of items, the number of relevance grades should also be small. First, having too much granularity in relevance level is not practical because data annotation can become easily unreliable and inconsistent (e.g., relevant:irrelevant vs. relevance Lv.36:relevance Lv.47). Relevance can also often be just naturally clustered even when defined with fine granularity.

Having too many levels is also not useful for model training. With the exponential NDCG, having too many levels can create extreme difference in relevance. This can make model training very unstable because the model will be overly incentivized to learn higher relevance items while essentially ignoring the distinction between low relevance items. This means training can be dominated by high-relevant items, making the fine granularity less useful. Model evaluation become even more challenging because it becomes extremely difficult to interpret ranking results and training process.

Summary

This post explores common pitfalls and practical considerations when working with ranking metrics. Compared to classification, ranking has the distinctive positional-discount feature, which results in many interesting metric definitions and important considerations around it. One of the main challenges with ranking evaluation is that metrics often do not capture the full picture of ranking because it almost always requires holistic understanding of item arrays. Given that there are many metrics to choose from and many parameters to tweak, understanding how the choice impacts use case and model training should help us make better decisions when designing and evaluating ranking systems.